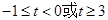题目
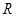 的函数
的函数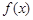 满足
满足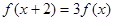 ,当
,当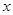 ∈
∈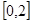 时,
时,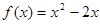
(1)当
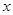 ∈
∈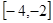 时,求
时,求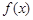 的解析式;
的解析式;(2)当x∈
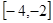 时,
时,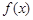 ≥
≥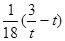 恒成立,求实数
恒成立,求实数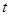 的取值范围.
的取值范围.
答案
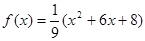 ;(2)
;(2)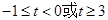
解析
试题分析:(1)由已知条件可求出f(x+4)=9f(x),设x∈[-4,-2],则4+x∈[0,2],由已知可得f(x+4)的解析式,即可得解.(2)首先求出
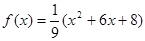 ,x∈
,x∈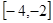 时的值域,由已知可得
时的值域,由已知可得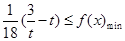 ,解不等式即可.
,解不等式即可.试题解析:(1)由f(x+2)=3f(x),得f(x+4)=3f(x+2)=9f(x),
设x∈[-4,-2],则4+x∈[0,2],∴f(x+4)=(x+4)2-2(x+4)=x2+6x+8,
因为f(x+4)=9f(x)
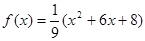 .
.(2)因为x∈
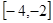 时,
时,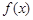 ≥
≥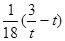 恒成立,所以x∈
恒成立,所以x∈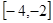 时,
时,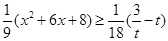 恒成立.而x∈
恒成立.而x∈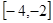 时,
时,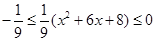 ,所以
,所以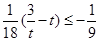 ,即
,即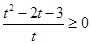 ,解得
,解得