题目
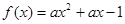 在
在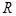 上满足
上满足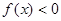 恒成立,则
恒成立,则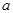 的取值范围
的取值范围是 。
答案
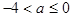
解析
试题分析:根据题意,要使得函数
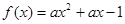 在
在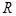 上满足
上满足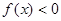 恒成立,那么当a=0时,则显然成立,当a
恒成立,那么当a=0时,则显然成立,当a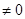 时,则可知只有开口向下,判别式小于零成立,即可知a<0,
时,则可知只有开口向下,判别式小于零成立,即可知a<0,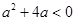 ,-4<a<0,综上可知满足题意的参数a的范围是
,-4<a<0,综上可知满足题意的参数a的范围是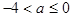 。
。点评:主要是考查了不等式恒成立问题,属于基础题。
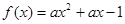 在
在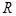 上满足
上满足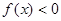 恒成立,则
恒成立,则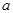 的取值范围
的取值范围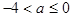
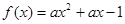 在
在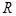 上满足
上满足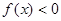 恒成立,那么当a=0时,则显然成立,当a
恒成立,那么当a=0时,则显然成立,当a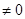 时,则可知只有开口向下,判别式小于零成立,即可知a<0,
时,则可知只有开口向下,判别式小于零成立,即可知a<0,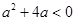 ,-4<a<0,综上可知满足题意的参数a的范围是
,-4<a<0,综上可知满足题意的参数a的范围是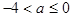 。
。