题目
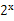 -2,若同时满足条件:
-2,若同时满足条件:①
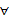 x∈R,f(x) <0或g(x) <0;②
x∈R,f(x) <0或g(x) <0;②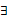 x∈(﹣∝, ﹣4),f(x)g(x) <0。求m的取值范围。
x∈(﹣∝, ﹣4),f(x)g(x) <0。求m的取值范围。
答案
 的取值范围为
的取值范围为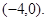
(二)综上所述满足①②两个条件的
 的取值范围为
的取值范围为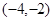
解析
试题分析:根据已知题意得到
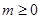 时不能保证对
时不能保证对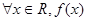 <0或
<0或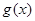 <0成立.
<0成立.那么只有m<0时,则根据二次函数图像与指数函数图像的位置关系,在满足前提条件下的,可知参数m的范围。
解:(一)由题意可知,
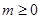 时不能保证对
时不能保证对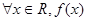 <0或
<0或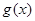 <0成立.
<0成立.⑴当
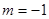 时,
时,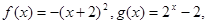 此时显然满足条件①;
此时显然满足条件①;
⑵当-1<
 <0时,
<0时,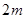 >
>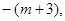 要使其满足条件①,则需-1<
要使其满足条件①,则需-1< <0且
<0且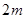 <1,解得-1<
<1,解得-1< <0;
<0; ⑶当
 <-1时,
<-1时,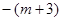 >
>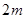 ,要使其满足条件①,则需
,要使其满足条件①,则需 <-1且
<-1且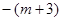 <1,
<1,解得-4<
 <-1. 因此满足条件①的
<-1. 因此满足条件①的 的取值范围为
的取值范围为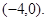
(二)在满足条件①的前提下,再探讨满足条件②的取值范围。
⑴当
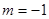 时,在
时,在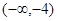 上,
上,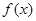 与
与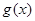 均小于0,不合题意;
均小于0,不合题意;⑵当
 <-1时,则需
<-1时,则需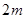 <-4,即
<-4,即 <-2,所以-4<
<-2,所以-4< <-2.
<-2.⑶当-1<
 <0时,则需
<0时,则需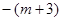 <-4,即
<-4,即 >1,此时无解。
>1,此时无解。综上所述满足①②两个条件的
 的取值范围为
的取值范围为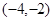
点评:解决该试题的关键是理解两个条件,翻译为图像中的二次函数中的两个根 的位置,以及对于m的分类讨论思想的运用。
