题目
已知数列{
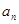 }满足
}满足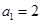 ,且点
,且点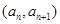 在函数
在函数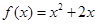 的图象上,其中
的图象上,其中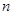 =1,2,3,….
=1,2,3,….(Ⅰ)证明:数列{lg(1+
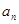 )}是等比数列;
)}是等比数列;(Ⅱ)设
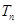 =(1+
=(1+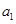 )(1+
)(1+ )…(1+
)…(1+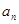 ),求
),求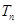 及数列{
及数列{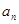 }的通项.
}的通项.
答案
(Ⅱ)由(Ⅰ)知lg(
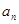 +1)=2n-1lg(1+
+1)=2n-1lg(1+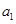 )
)=2n-1lg3=lg
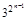 .∴
.∴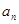 +1=
+1=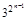 . 则
. 则 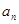 =
= 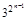 -1
-1 ∴
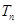 =(1+
=(1+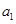 )(1+
)(1+ )…(1+
)…(1+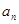 )=
)=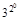 ·
·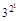 ·
·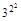 ·…·
·…·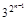
=
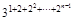 =
=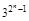 .∴
.∴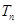 =
=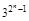 ,
,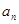 =
=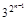 -1.
-1.
解析
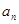 ,
,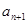 )在函数
)在函数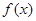 的图象上,
的图象上,可得
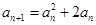 ,从而可得
,从而可得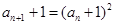 ,
,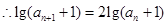 ,从而得到证明.
,从而得到证明.(II)求出
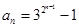 ,然后可知
,然后可知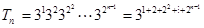 然后再利用等比数列前n项和公式求解.
然后再利用等比数列前n项和公式求解.(Ⅰ)证明: 由于(
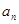 ,
,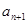 )在函数
)在函数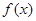 的图象上,
的图象上, ∴
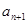 =
=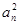 +2
+2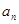 ,∴
,∴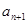 +1=
+1= . …………4分
. …………4分∵
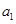 =2,∴
=2,∴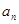 +1﹥1,∴lg(
+1﹥1,∴lg(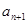 +1)=2lg(
+1)=2lg(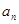 +1).
+1).∴数列{lg(
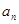 +1)}是公比为2的等比数列. …………6分
+1)}是公比为2的等比数列. …………6分(Ⅱ)解: 由(Ⅰ)知lg(
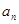 +1)=2n-1lg(1+
+1)=2n-1lg(1+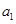 )
)=2n-1lg3=lg
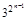 .∴
.∴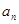 +1=
+1=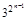 . 则
. 则 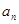 =
= 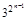 -1 …………9分
-1 …………9分∴
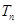 =(1+
=(1+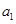 )(1+
)(1+ )…(1+
)…(1+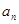 )=
)=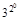 ·
·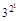 ·
·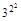 ·…·
·…·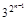
=
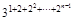 =
=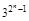 .∴
.∴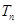 =
=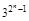 ,
,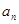 =
=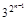 -1. …………12分
-1. …………12分
