题目

(本小题满分14分)函数f(x)＝1－2a－2acosx－2sin²x的最小值为g(a)(a∈R)．
(1)求g(a)；
(2)若g(a)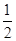＝，求a及此时f(x)的最大值．

答案

（1）见解析；(2)a＝－1. 此时f(x)取得最大值为5.

解析

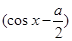(1)f(x)＝1－2a－2acosx－2sin²x＝2²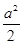－－2a－1.－1≤cosx≤1.转化为二次函数问题解决.
(2)在第（1）问的基础上，根据g(a)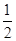＝，建立关于a的方程求解即可.
解：(1)由f(x)＝1－2a－2acosx－2sin²x
＝1－2a－2acosx－2(1－cos²x)
＝2cos²x－2acosx－(2a＋1)
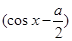＝2²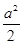－－2a－1.这里－1≤cosx≤1.…………4分 
①若－1≤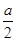≤1，即－2≤a≤2，则当cosx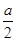＝时，f(x)_min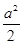＝－－2a－1；…………5分 
②若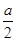>1，则当cosx＝1时，f(x)_min＝1－4a；…………6分 
③若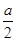<－1，则当cosx＝－1时，f(x)_min＝1.…………7分
因此g(a)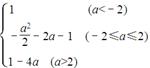＝.…………8分
(2)∵g(a)＝.
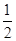∴①若a>2，则有1－4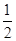a＝，得a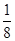＝，矛盾；…………10分
②若－2≤a≤2，则有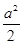－－2a－1＝，
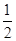即a²＋4a＋3＝0，∴a＝－1或a＝－3(舍)． …………12分
∴g(a)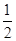＝时，a＝－1. 此时f(x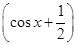)＝2²＋，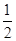
当cosx＝1时，f(x)取得最大值为5.…………14分