题目
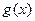 对
对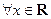 都满足
都满足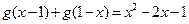 且
且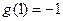 ,设函数
,设函数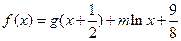
(
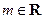 ,
,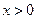 ).
).(1)求
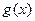 的表达式;
的表达式;(2)若
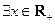 ,使
,使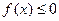
 成立,求实数
成立,求实数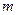 的取值范围;
的取值范围;(3)设
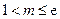 ,
, ,求证:对于
,求证:对于 ,恒有
,恒有 .
.
答案
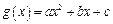 ,于是
,于是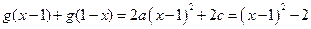 ,所以
,所以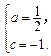
又
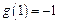 ,则
,则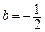 .所以
.所以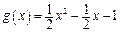 .
.(2)
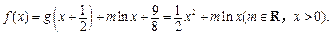
当m>0时,由对数函数性质,f(x)的值域为R;
当m=0时,
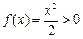 对
对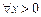 ,
,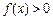 恒成立;
恒成立; 当m<0时,由
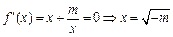 ,
,列表:
| x |
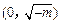 |
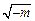 |
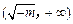 |
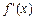 |
- |
0 |
+ |
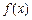 |
递减 |
极小值 |
递增 |
这时
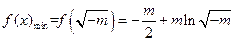 ,
,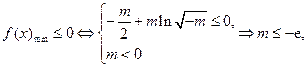
综上,
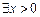 使
使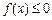 成立,实数m的取值范围
成立,实数m的取值范围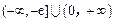 .
.(3)由题知
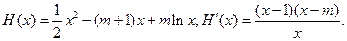 因为对
因为对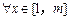 ,
,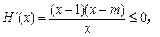 所以
所以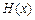 在
在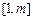 内单调递减.
内单调递减.于是
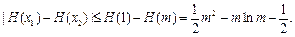

记
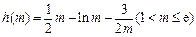 ,则
,则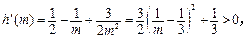
所以函数
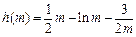 在
在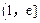 是单调增函数,
是单调增函数, 所以
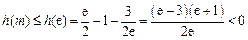 ,故命题成立.
,故命题成立.
