题目

（本题11分）如图，矩形ABCD中，AB=6，BC=2，点O是AB的中点，点P在AB的延长线上，且BP=3．一动点E从O点出发，以每秒1个单位长度的速度沿OA匀速运动，到达A点后，立即以原速度沿AO返回；另一动点F从P点出发，以每秒1个单位长度的速度沿射线PA匀速运动，点E、F同时出发，当两点相遇时停止运动，在点E、F的运动过程中，以EF为边作等边△EFG，使△EFG和矩形ABCD在射线PA的同侧．设运动的时间为t秒（t≥0）．
（1）当等边△EFG的边FG恰好经过点C时，求运动时间t的值；
（2）在整个运动过程中，设等边△EFG和矩形ABCD重叠部分的面积为S，求出S与t之间的函数关系式和相应的自变量t的取值范围；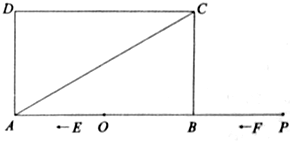

答案

解：（1）当边FG恰好经过点C时，∠CFB=60°，BF=3﹣t，在Rt△CBF中，BC=2，tan∠CFB=，即tan60=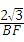，解得BF=2，即3﹣t=2，t=1，∴当边FG恰好经过点C时，t=1；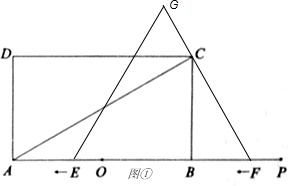
（2）当0≤t＜1时，S=2t+4；
当1≤t＜3时，S=﹣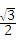t²+3t+；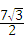
当3≤t＜4时，S=﹣4t+20；
当4≤t＜6时，S=t²﹣12t+36；

解析

略