题目

已知函数f(x)=ax²+bx+c(a>0)，α、β为方程f(x)=x的两根，且0<α<β<，
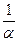0<x<α，给出下列不等式，其中成立的是                                                （   ）
①x<f(x)                          ②α<f(x)                 ③x>f(x)                  ④α>f(x)

A．①④

B．③④

C．①②

D．②④

答案

A

解析

设F(x)=f(x)-x，由已知α、β是F(x)=0的两根，∴F(x)=a(x-α)(x-β).
在x∈（0，α）时，f(x)-x=F(x)=a(x-α)(α-β).
∵a>0，x-α<0，x-β<0，∴F(x)>0.∴f(x)>x.
又a-f(x)=α-[F(x)+x]=α-x-F(x)=α-x-a(x-α)(x-β)=(α-x)[1+a(α-β)].
∵0<x<α<β<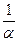，∴aβ<1.∴1+a(x-β)=1+ax-aβ>1-aβ>0.
而α-x>0，∴α-f(x)>0.∴f(x)<α. 故选A．