题目
已知函数
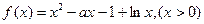
(1)当
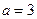 时,求
时,求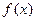 的单调递增区间;
的单调递增区间;(2)若
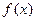 在
在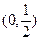 上是增函数,求
上是增函数,求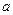 的取值范围;
的取值范围;(3)是否存在实数
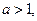 使得方程
使得方程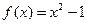 在区间
在区间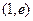 上有解,若存在,
上有解,若存在,试求出
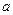 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
答案
(1)
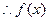 单调增区间为
单调增区间为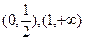
(2)
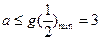
(3)不存在
解析
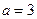 时,
时,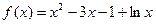
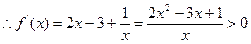 ,解得
,解得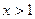 或
或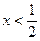 ,又
,又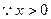
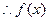 单调增区间为
单调增区间为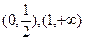
(2)若
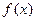 在
在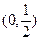 上是增函数,则对任意
上是增函数,则对任意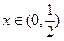 ,
,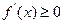 恒成立,
恒成立,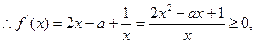 等价于:
等价于: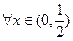 ,
,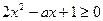 恒成立,等价于:
恒成立,等价于: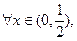
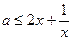 恒成立
恒成立令
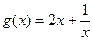 ,
,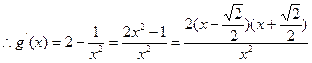
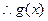 在
在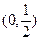 上为减函数,
上为减函数,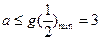
(3)假设
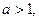 方程
方程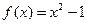 在区间
在区间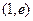 有解,等价转化为:
有解,等价转化为:当
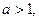 函数
函数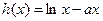 在区间
在区间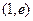 上有零点
上有零点令
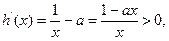 解得:
解得: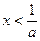 ,又
,又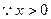 ,
,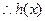 单调增区间为
单调增区间为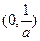 ,单调减区间
,单调减区间 ,
,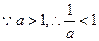 ,
,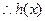 在
在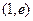 上为减区间,而
上为减区间,而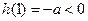 ,
,故
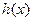 在
在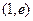 上不存在零点
上不存在零点
