题目

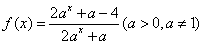已知函数是定义在R上的奇函数。
（1）求实数a的值；
（2）判断f(x)在定义域上的单调性，并用单调性定义证明；
（3）当x∈(0，1]时，t·f(x) ≥2^x-2恒成立，求实数t的取值范围。

答案

解：（1），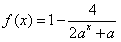
令x=0，则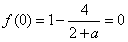，∴a=2，
经检验a=2时，f（x）为定义在R上的奇函数。
（2）f(x)是R上的增函数。
证明：任取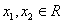，且，
∴，
∵，
∴，，
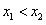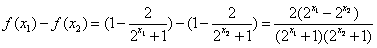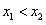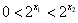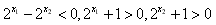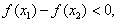∴即，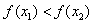
所以f(x)是R上的增函数。
（3）不等式，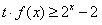
∴，
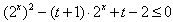令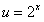，x∈(0，1]，则u∈(1，2]，
于是，当x∈(0，1]时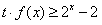，恒成立，
即当u∈(1，2]时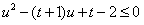，恒成立；
令，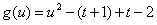
∴，
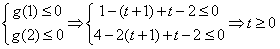所以实数t的取值范围是。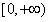

解析