题目

设
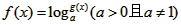
(1)若f（x）在定义域D内是奇函数，求证：g（x）·g（-x）=1 ；
(2)若g（x）=ax且在[1，3]上，f（x）的最大值是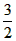，求实数a的值
(3)若g（x）=ax²-x，是否存在实数a，使得f（x）在区间I=[2，4]上是减函数？且对任意的x₁，x₂∈I都有
f(x)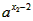＞，如果存在，说明a可以取哪些值；如果不存在，请说明理由。

答案

解：（1）∵f（x）在定义域D内是奇函数
∴f（x）+f（-x）=0
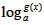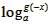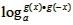+=0即=0
∴g（x）·g（-x）=1
（2）①若a＞1，则f（x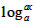）=在[1，3]上是增函数，则有f(3)=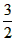
∴f（x）==
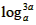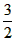
∴a=9
②若0＜a＜1，则在[1，3]上是减函数，则有f(1)=
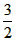
∴f（x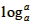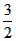）==，解得：a不存在
综上所述：a=9
（3）①若a＞1时，要满足题设，则有g（x）=ax²-x在[2，4]上是减函数。
∴而函数g（x）=ax²-x＞0仅在（-∞，0）上是减函数，
 故a＞1不符合题意
另解：①当a＞1时，可知g（x）=ax²-x在[2，4]上是增函数，而函数y=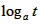是增函数，故f（x）在区间
I=[2，4]上是增函数，与已知矛盾，舍去。
②若0＜a＜1时，要满足题设，则有g（x）=ax²-x在[2，4]上是增函数，并且g（x）>0在[2，4]上成立，
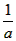∴<2，∴a>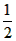
要对任意的x₁，x₂∈I都有f(x)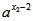＞，只要求f(x)的最小值大于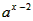的最大值即可。
∵f（x）在区间I=[2，4]上是减函数，
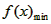∴ =f（4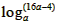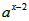）=，的最大值为a⁰=1
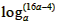∴>1，∴a<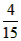，这与a>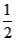矛盾，舍去
综上所述：满足题设的实数a不存在。

解析