题目

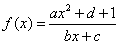已知函数，g(x)=ax³+cx²+bx+d都是奇函数，其中a，b，c，d∈Z，且f(1)=2，f(2)＜3，
（1）求a，b，c，d的值；
（2）求证：g(x)在R上是增函数。

答案

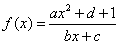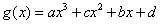（1）解：因为函数，都是奇函数，
所以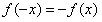，，解得：c=0；
由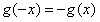，得d=0；
由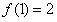，得a=2b-1，
代入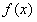中，得，
，
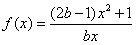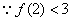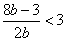∴即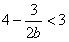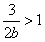，，所以b＞0，由此可解得：，
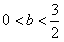考虑到a，b，c，d∈Z，所以b=1，所以a=2b-1=1，
综上知：a=1，b=1，c=0，d=0。
（2）证明：，
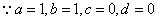所以函数，
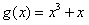任取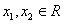，且，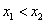
∴


，
，，
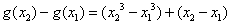
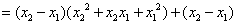
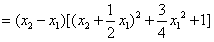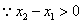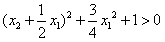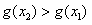∴，即g（x）在R上是增函数。

解析