题目
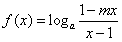 是奇函数(a>0, 且a≠1)。
是奇函数(a>0, 且a≠1)。(1)求m的值;
(2)判断f(x)在区间(1,+∞)上的单调性并加以证明;
(3)当a>1,x∈(r,a-2)时,f(x)的值域是(1,+∞),求a与r的值。
答案
解:(1)由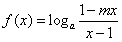 是奇函数,得f(-x)=-f(x),
是奇函数,得f(-x)=-f(x),
即loga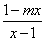 +loga
+loga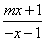 =0,
=0,
∴loga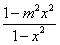 =0,解得:m=-1(m=1舍去)。
=0,解得:m=-1(m=1舍去)。
(2)由(1)得,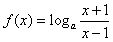 (a>0,a≠1),
(a>0,a≠1),
任取x1,x2∈(1,+∞),且x1<x2,
令t(x)=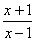 , 则
, 则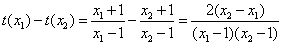 ,
,
∵x1>1,x2>1,x1<x2,
∴x1-1>0,x2-1>0,x2-x1>0,
∴t(x1)>t(x2),
∴当a>1时,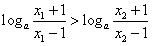 ,f(x)在(1,+∞)上是减函数;
,f(x)在(1,+∞)上是减函数;
当0<a<1时,f(x)在(1,+∞)上是增函数。
(3)当a>1时,要使f(x)的值域是(1,+∞),则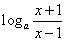 >1,即
>1,即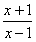 >a,
>a,
从而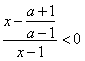 ,
,
又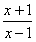 >1,即
>1,即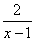 >0,解得:x>1,
>0,解得:x>1,
∴1<x<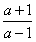 ,
,
∴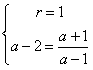 ,∴r=1,a=2+
,∴r=1,a=2+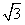 。
。
