题目

设函数f(x)对于x，y∈R都有f(x+y)=f(x)+f(y)，且x＞0时，f(x)＜0，f(1)=-2。
（1）说明函数f(x)是奇函数还是偶函数？
（2）探究f(x)在[-3，3]上是否有最值？若有，请求出最值，若没有，说明理由；
（3）若f(x)的定义域是[-2，2]，解不等式：。

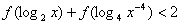答案

解：（1）设y=x=0，有，
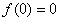取y=-x，则有，
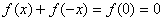
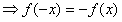∴f(x)是奇函数。
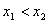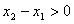（2）设，则，由条件得，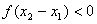
∴，
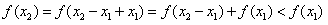∴f(x)在R上是减函数，在[-3，3]上也是减函数，
∴f(x)当x=-3时有最大值f(-3)；当x=3时有最小值f(3)；
由，，
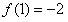
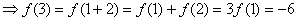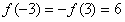∴f(x)当x=-3时有最大值6；当x=3时有最小值-6。
（3）由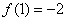，f(x)是奇函数，∴，
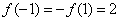原不等式就是，
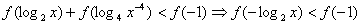由（2）知f(x)在[-2，2]上是减函数，
，
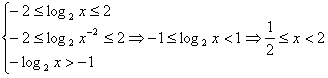∴原不等式的解集是。

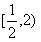解析