题目
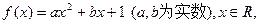
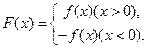
(1)若不等式
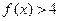 的解集为
的解集为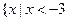 或
或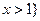 ,求
,求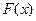 的表达式;
的表达式;(2)在(1)的条件下, 当
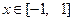 时,
时, 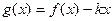 是单调函数, 求实数k的取值范围;
是单调函数, 求实数k的取值范围;(3)设
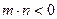 ,
, 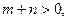
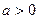 且
且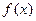 为偶函数, 判断
为偶函数, 判断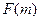 +
+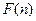 能否大于零?
能否大于零?
答案
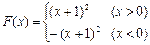
(2)
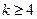 或
或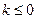
(3)
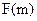 +
+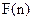 能大于零.
能大于零.
解析
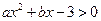 的解集为
的解集为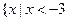 或
或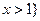 ,故
,故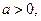 且方程
且方程 的两根为
的两根为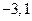 ,由韦达定理,得
,由韦达定理,得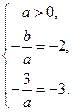 解得
解得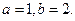 因此,
因此,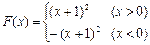
(2) 则
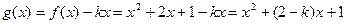
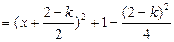 ,
, 当
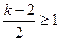 或
或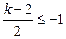 时, 即
时, 即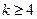 或
或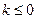 时,
时, 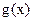 是单调函数.
是单调函数.(3) ∵
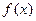 是偶函数∴
是偶函数∴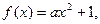
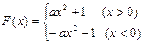 ,
, ∵
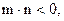 设
设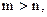 则
则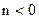 .又
.又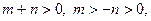 ∴
∴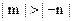
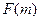 +
+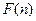
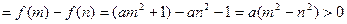 ,
,∴
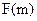 +
+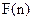 能大于零.
能大于零.
