题目
 函数
函数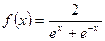 .
.(Ⅰ) 判断函数
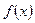 的奇偶性,并求其最大值;
的奇偶性,并求其最大值;(Ⅱ) 求证:
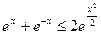 ;
;(Ⅲ) 求证:
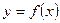 的图象
的图象 与
与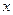 轴所围成的图形的面积不小于
轴所围成的图形的面积不小于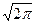 .
.
答案
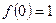
(Ⅱ)证明见解析
(Ⅲ)证明见解析
解析
(Ⅰ)定义域为
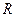 ,
,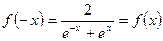 ,则
,则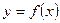 为偶函数,
为偶函数,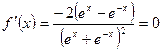 ,则
,则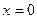 ,
,所以函数
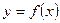 在
在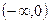 上单调递增,在
上单调递增,在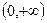 上单调递减,
上单调递减,则最大值
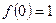 ;------------------------------------------------------
;------------------------------------------------------ 4分
4分(Ⅱ)要证明
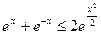 ,
,只
 需证
需证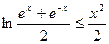 ,
,设

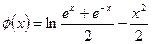 ,
,则
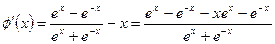
令
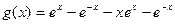
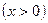 ,则
,则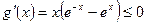
所以,
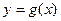 在
在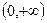 上为单调递减函数,
上为单调递减函数,因此,
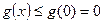
所以当
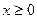 时,
时,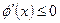 ,又因为
,又因为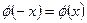 ,则
,则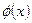 为偶函数,
为偶函数,所以
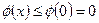 ,则原结论成立;-
,则原结论成立;- ---------------------------------------8分
---------------------------------------8分(Ⅲ)由标准正态分布
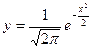 与
与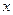 轴围成的面积为
轴围成的面积为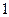 ,
,则由(Ⅱ)得
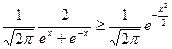 ,
,则
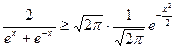 ,
,所以
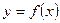 的图象与
的图象与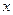 轴所围成的图形的面积不小于
轴所围成的图形的面积不小于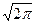 .------------------12分
.------------------12分
