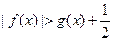题目
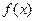 是定义在
是定义在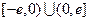 上的奇函数,当
上的奇函数,当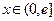 时
时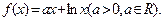
(Ⅰ)求
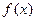 的解析式;
的解析式;(Ⅱ)设
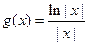 ,
,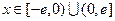 ,求证:当
,求证:当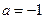 时,
时,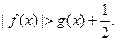
答案
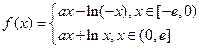
解析
(Ⅰ)设
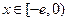 ,则
,则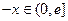 ,
,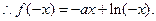
又
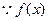 是定义在
是定义在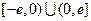 上的奇函数,
上的奇函数,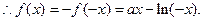
故函数的解析式为:
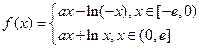
(Ⅱ)
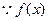 是奇函数,
是奇函数,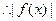 是偶函数,又
是偶函数,又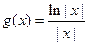 是偶函数
是偶函数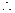 只要证明当
只要证明当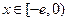 时,
时,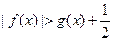 即可.
即可.证明如下:当
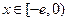 时,
时,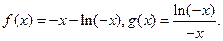
设
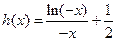
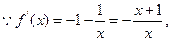 见下表
见下表
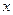 |
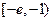 |
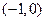 |
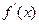 |
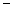 |
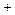 |
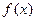 |
递减 |
递增 |
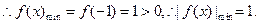
又
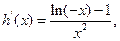 当
当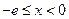 时,
时,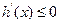 ,此时
,此时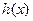 单调递减
单调递减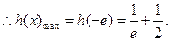 而
而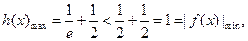
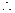 当
当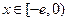 时,
时,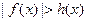 ,即
,即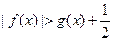
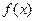 是定义在
是定义在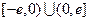 上的奇函数,当
上的奇函数,当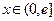 时
时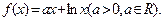
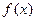 的解析式;
的解析式;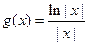 ,
,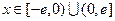 ,求证:当
,求证:当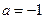 时,
时,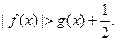
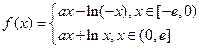
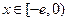 ,则
,则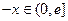 ,
,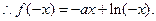
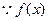 是定义在
是定义在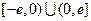 上的奇函数,
上的奇函数,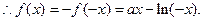
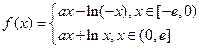
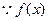 是奇函数,
是奇函数,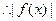 是偶函数,又
是偶函数,又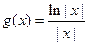 是偶函数
是偶函数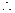 只要证明当
只要证明当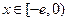 时,
时,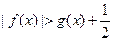 即可.
即可.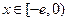 时,
时,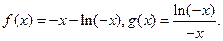
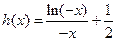
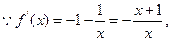 见下表
见下表
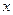 |
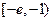 |
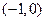 |
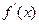 |
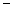 |
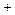 |
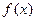 |
递减 |
递增 |
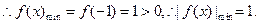
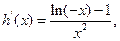 当
当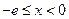 时,
时,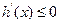 ,此时
,此时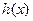 单调递减
单调递减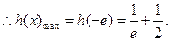 而
而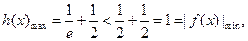
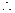 当
当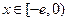 时,
时,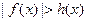 ,即
,即