题目
 的定义域为
的定义域为 ,若存在非零实数
,若存在非零实数 使得对于任意
使得对于任意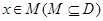 ,有
,有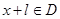 ,且f(x+l)≥f(x),则称
,且f(x+l)≥f(x),则称 为
为 上的
上的 高调函数.如果定义域是
高调函数.如果定义域是 的函数
的函数 为
为 上的
上的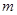 高调函数,那么实数
高调函数,那么实数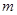 的取值范围是 [2,+∞)_
的取值范围是 [2,+∞)_如果定义域为
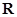 的函数
的函数 是奇函数,当x≥0时,
是奇函数,当x≥0时,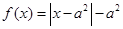 ,且
,且 为
为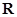 上的
上的 高调函数,那么实数
高调函数,那么实数 的取值范围是__________.
的取值范围是__________.
答案
解析
 为
为 上的
上的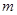 高调函数,首先,
高调函数,首先, 时
时 ,所以
,所以 。同时有
。同时有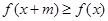 对任意
对任意 恒成立;即
恒成立;即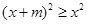 对
对 恒成立,也就是
恒成立,也就是 对
对 恒成立。又
恒成立。又 ,只需
,只需 在
在 恒成立,故
恒成立,故 ,所以实数
,所以实数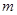 的取值范围是
的取值范围是 。
。(2)
 时,
时,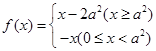 ,又函数
,又函数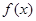 式定义在R 上的奇函数,所以
式定义在R 上的奇函数,所以 其图像如图:
其图像如图: 
 是由
是由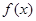 向左平移4个单位得到的;所以要使
向左平移4个单位得到的;所以要使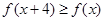 恒成立,需使
恒成立,需使 。解得
。解得 ,故实数
,故实数 的取值范围是[-1,1]
的取值范围是[-1,1]
