题目
设函数
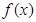 对任意实数
对任意实数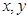 都有
都有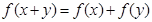 且
且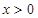 时
时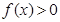 。
。(Ⅰ)证明
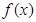 是奇函数;
是奇函数;(Ⅱ)证明
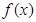 在
在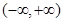 内是增函数;
内是增函数;(Ⅲ)若
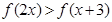 ,试求
,试求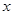 的取值范围。
的取值范围。
答案
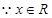 ,
, 函数
函数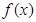 的定义域关于原点对称,
的定义域关于原点对称,令
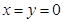 ,则
,则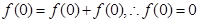 ,
,令
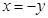 ,则
,则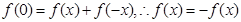 ,
, 函数
函数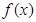 为奇函数。(4分)
为奇函数。(4分)(Ⅱ)证明:设
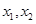 是
是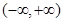 内任意两实数,且
内任意两实数,且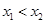 ,则
,则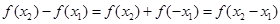 ,
,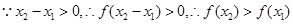 ,
, 函数
函数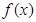 在
在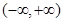 内是增函数。(4分)
内是增函数。(4分)(Ⅲ)解:
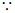 函数
函数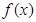 在
在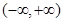 内是增函数,且
内是增函数,且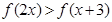 ,
,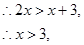

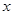 的取值范围为
的取值范围为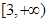 。(4分)
。(4分)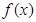 对任意实数
对任意实数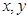 都有
都有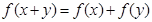 且
且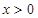 时
时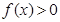 。
。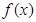 是奇函数;
是奇函数;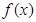 在
在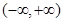 内是增函数;
内是增函数;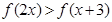 ,试求
,试求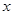 的取值范围。
的取值范围。
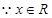 ,
, 函数
函数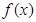 的定义域关于原点对称,
的定义域关于原点对称,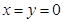 ,则
,则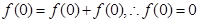 ,
,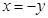 ,则
,则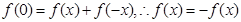 ,
, 函数
函数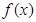 为奇函数。(4分)
为奇函数。(4分)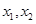 是
是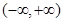 内任意两实数,且
内任意两实数,且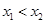 ,则
,则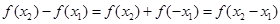 ,
,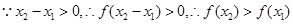 ,
, 函数
函数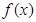 在
在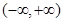 内是增函数。(4分)
内是增函数。(4分)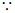 函数
函数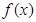 在
在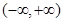 内是增函数,且
内是增函数,且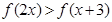 ,
,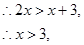

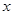 的取值范围为
的取值范围为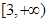 。(4分)
。(4分)