题目
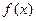 是定义在
是定义在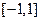 上的奇函数,且
上的奇函数,且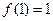 ,若
,若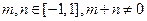 时,有
时,有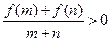
 .
.(1)解不等式
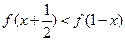 ;
;(2)若
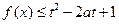 对所有
对所有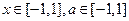 恒成立,求实数
恒成立,求实数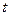 的取值范围.
的取值范围.
答案
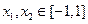 且
且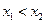 ,则
,则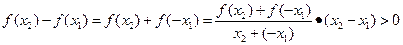
∴
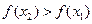 ,∴
,∴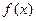 为增函数
为增函数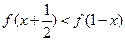
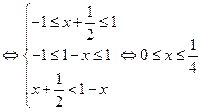 ,
,即不等式
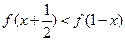 的解集为
的解集为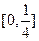 .
.(2)由于
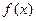 为增函数,∴
为增函数,∴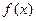 的最大值为
的最大值为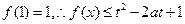 对
对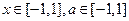 恒成立
恒成立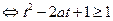 对任意的
对任意的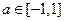 恒成立
恒成立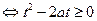 对任意的
对任意的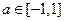 恒成立。
恒成立。把
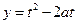 看作
看作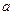 的函数,由于
的函数,由于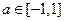 知其图像是一条线段。
知其图像是一条线段。∴
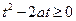 对任意的
对任意的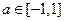 恒成立
恒成立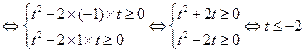 或
或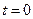 或
或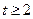 .
.
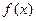 是定义在
是定义在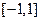 上的奇函数,且
上的奇函数,且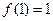 ,若
,若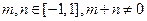 时,有
时,有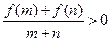
 .
.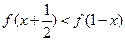 ;
;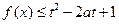 对所有
对所有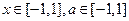 恒成立,求实数
恒成立,求实数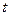 的取值范围.
的取值范围.
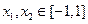 且
且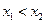 ,则
,则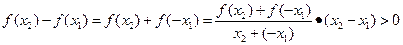
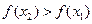 ,∴
,∴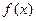 为增函数
为增函数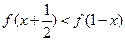
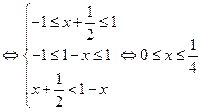 ,
,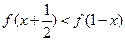 的解集为
的解集为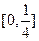 .
.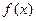 为增函数,∴
为增函数,∴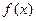 的最大值为
的最大值为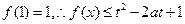 对
对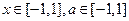 恒成立
恒成立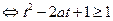 对任意的
对任意的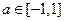 恒成立
恒成立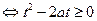 对任意的
对任意的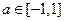 恒成立。
恒成立。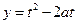 看作
看作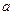 的函数,由于
的函数,由于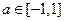 知其图像是一条线段。
知其图像是一条线段。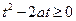 对任意的
对任意的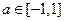 恒成立
恒成立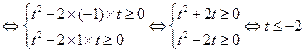 或
或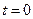 或
或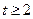 .
.