题目
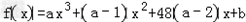 的图象关于原点成中心对称,试判断
的图象关于原点成中心对称,试判断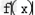 在区间[﹣4,4]上的单调性,并证明你的结论.
在区间[﹣4,4]上的单调性,并证明你的结论.答案
证明如下:函数f(x)的图象关于原点成中心对称,则f(x)是奇函数,
即f(﹣x)=﹣f(x)对于任意x的成立,
则有a(﹣x)3+(a﹣1)(﹣x)2+48(a﹣2)(﹣x)x+b
=﹣[ax3+(a﹣1)x2+48(a﹣2)x+b]
必有a﹣1=0,b=0,即a=1,b=0,
于是f(x)=x3﹣48x.
∴
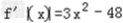 ,
,∴当
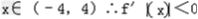 ,
,所以f(x)在[﹣4,4]上是单调递减函数.
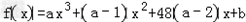 的图象关于原点成中心对称,试判断
的图象关于原点成中心对称,试判断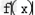 在区间[﹣4,4]上的单调性,并证明你的结论.
在区间[﹣4,4]上的单调性,并证明你的结论.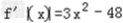 ,
,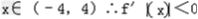 ,
,