题目
(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性;
(3)求
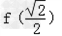 的值.
的值.答案
解:(1)∵1+x>0且1﹣x>0
∴x∈(﹣1,1),
∴函数的定义域为(﹣1,1);
(2)∵f(﹣x)=log2(1﹣x)+log2(1+x)=f(x)
∴f(x)为偶函数;
(3)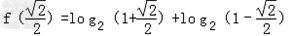
=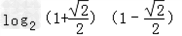
=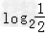 =﹣1.
=﹣1.
所以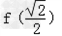 的值为:﹣1.
的值为:﹣1.
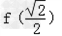 的值.
的值.解:(1)∵1+x>0且1﹣x>0
∴x∈(﹣1,1),
∴函数的定义域为(﹣1,1);
(2)∵f(﹣x)=log2(1﹣x)+log2(1+x)=f(x)
∴f(x)为偶函数;
(3)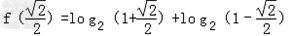
=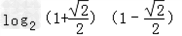
=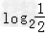 =﹣1.
=﹣1.
所以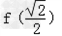 的值为:﹣1.
的值为:﹣1.