题目

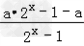若函数y=为奇函数．
（1）求a的值；
（2）求函数的定义域；
（3）讨论函数的单调性．

答案

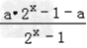解：（1）∵函数y=f（x）= 为奇函数，
∴f（﹣x）+f（x）=0
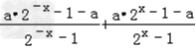∴ =0
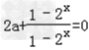∴  ∴a=﹣ 
（2）f（x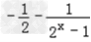）= ，∴2x﹣1≠0，
∴2x≠1，∴x≠0
∴函数的定义域为（﹣∞，0）∪（0，+∞）
（3）f（x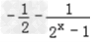）= 在（﹣∞，0）和（0，+∞）上为增函数
证明：任取x₁，x₂∈（0，+∞），且x₁＜x₂，
则2x₁＜2x₂，2x₁﹣1＞0，2x₂﹣1＞0，
∴f（x₁）﹣f（x₂）
=（ ）﹣（ ）
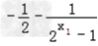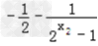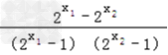= ＜0，
∴f（x₁）＜f（x₂），
∴f（x）在（0，+∞）上为增函数．
任取x₁，x₂∈（﹣∞，0）且x₁＜x₂，则﹣x₁＞﹣x₂＞0，
因为f（x）在（0，+∞）上为增函数，所以f（﹣x₁）＞f（﹣x₂），
因为f（x）是奇函数，所以f（﹣x₁）=﹣f（x₁），f（﹣x₂）=﹣f（x₂），
∴﹣f（x₁）＞﹣f（x₂），∴f（x₁）＜f（x₂），
∴f（x）在（﹣∞，0）上为增函数．

解析