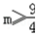
题目

已知定义在R上的函数f（x）满足下面两个条件：
①对于任意的x，y∈R，都有f（x+y）=f（x）+f（y）
②当x＞0时，f（x）＜0
（1）判断f（x）的奇偶性，并证明；
（2）判断f（x）的单调性，并证明；
（3）如果不等式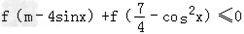对于任意x∈R都成立，求实数m的取值范围．

答案

解：（1）取x=y=0，可得f（0）=0，
再取y=﹣x，可得f（x）+f（﹣x）=f（0）=0，
所以f（﹣x）=﹣f（x），f（x）是奇函数 
（2）任取x₁＜x₂，则 f（x₂）﹣f（x₁）=f（x₂）+f（﹣x₁）=f（x₂﹣x₁）＜0，
可得 f（x₁）＞f（x₂），所以f（x） 在R上是减函数
（3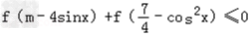）∵ ，且f（x）是奇函数
∴ 
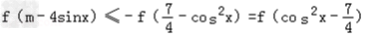
∵f（x） 在R上是减函数
∴ ，即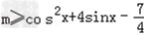 
∴ 
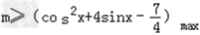
∴下面即求函数 的最大值
由于 = 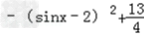，sinx∈[﹣1，1]
∴当且仅当sinx=1时， = 
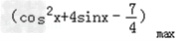所以 

解析