题目

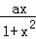已知函数f（x）=（a≠0）．
（1）判断并证明函数的奇偶性；
（2）当a=1时，用定义证明函数在[﹣1，1]上是增函数；
（3）求函数在，[﹣1，1]上的最值．

答案

证明：（1）由题意，函数f（x）的定义域为R，
对任意x∈R都有f（﹣x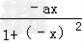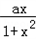）==﹣=﹣f（x），
故f（x）在R上为奇函数；
（2）任取﹣1≤x₁＜x₂≤1则f（x₁）﹣f（x₂）=
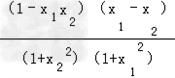
∵﹣1≤x₁＜x₂≤1，
∴x₁﹣x₂＜0，x₁x₂＜1，
∴f（x₁）﹣f（x₂）＜0，
∴f（x₁）＜f（x₂）．
故f（x）在[﹣1，1]上为增函数；
（3）由（1）（2）可知：
①当a＞0时，f（x）在[﹣1，1]上为增函数，
故f（x）在[﹣1，1]上的最大值为f（1）=，最小值为f（﹣1）=﹣，
②当a＜0时，f（x）在[﹣1，1]上为减函数，
故f（x）在[﹣1，1]上的最大值为f（﹣1）=﹣，最小值为f（1）=，

解析