题目
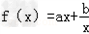 ,且f(1)=2,
,且f(1)=2,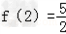
(2)判断函数f(x)的奇偶性;
(3)判断f(x)在(1,+∞)上的单调性并加以证明.
答案
 ,得
,得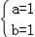
(2)
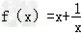 的定义域为(﹣
的定义域为(﹣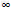 ,0)
,0)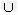 (0,+
(0,+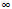 )关于原点对称,
)关于原点对称,
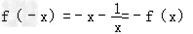
 函数f(x)为奇函数.
函数f(x)为奇函数.(3)f(x)在(1,+
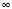 )上是增函数,
)上是增函数,证明如下设x1,x2
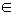 (1,+
(1,+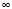 ),且x1<x2
),且x1<x2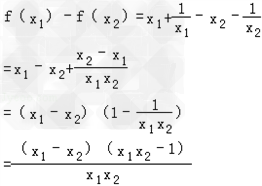
 x1,x2
x1,x2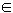 (1,+
(1,+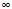 )且x1<x2
)且x1<x2 x1﹣x2<0,x1x2>1,x1x2﹣1>0
x1﹣x2<0,x1x2>1,x1x2﹣1>0 f(x1)﹣f(x2)<0,即f(x1)<f(x2)
f(x1)﹣f(x2)<0,即f(x1)<f(x2) f(x)在(1,+
f(x)在(1,+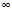 )上是增函数.
)上是增函数. 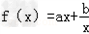 ,且f(1)=2,
,且f(1)=2,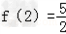
 ,得
,得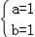
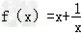 的定义域为(﹣
的定义域为(﹣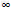 ,0)
,0)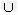 (0,+
(0,+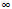 )关于原点对称,
)关于原点对称,
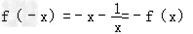
 函数f(x)为奇函数.
函数f(x)为奇函数.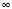 )上是增函数,
)上是增函数,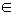 (1,+
(1,+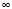 ),且x1<x2
),且x1<x2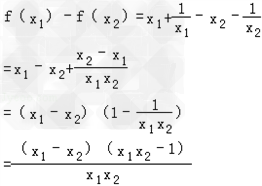
 x1,x2
x1,x2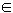 (1,+
(1,+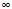 )且x1<x2
)且x1<x2 x1﹣x2<0,x1x2>1,x1x2﹣1>0
x1﹣x2<0,x1x2>1,x1x2﹣1>0 f(x1)﹣f(x2)<0,即f(x1)<f(x2)
f(x1)﹣f(x2)<0,即f(x1)<f(x2) f(x)在(1,+
f(x)在(1,+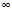 )上是增函数.
)上是增函数.