题目

已知函数f（x）=ln（e^x+k）（k为常数）是实数集R上的奇函数 （1）求k的值
（2）若函数g（x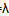）=f（x）+sinx是区间[﹣1，1]上的减函数，且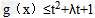在x[﹣1，1]上恒成立，求t的取值范围
（3）讨论关于x的方程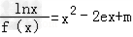的根的个数．

答案

解：（1）因为函数f（x）=ln（e^x+k）（k为常数）是实数集R上的奇函数，
所以f（﹣0）=﹣f（0）
即f（0）=0，
则ln（e⁰+k）=0解得k=0，
显然k=0时，f（x）=x是实数集R上的奇函数；
（2）由（1）得f（x）=x所以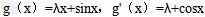
因为g（x） 在[﹣1，1]上单调递减，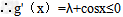
在[﹣1，1]上恒成立，
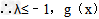_max=g（﹣1）=﹣1﹣sin1，
只需，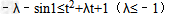
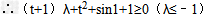恒成立，
令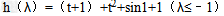
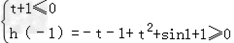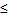则解得t﹣1
（3）由（1）得f（x）=x
方程转化为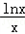=x²﹣2e^x+m，
令F（x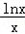）=（x＞0），G（x）=x²﹣2e^x+m（x＞0），
F"（x）=，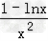
令F"（x）=0，
即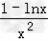=0，得x=e
当x（0，e）时，F"（x）＞0，F（x）在（0，e）上为增函数；
当x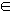（e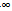，+）时，F"（x）＜0，F（x）在（e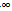，+）上为减函数；
当x=e时，F（x）_max=F（e）=
而G（x）=（x﹣e）²+m﹣e²   （x＞0）
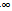G（x）在（0，e）上为减函数，在（e，+）上为增函数；
当x=e时，G（x）_min=m﹣e²
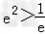当m﹣，即m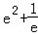＞时，方程无解；
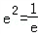当m﹣，即m=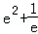时，方程有一个根；
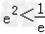当m﹣，即m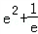＜时，方程有两个根；

解析