题目

已知定义在R上的函数f（x）满足f（1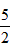）=，且对于任意实数x，y，总有f（x）·f（y）= f（x+y）+f（x-y）成立。
（Ⅰ）求f（0）的值，并证明函数f（x）为偶函数；
（Ⅱ）定义数列{a_n}：a_n=2f（n+1）-f（n）（n=1，2，3，…），求证：数列{a_n}为等比数列。

答案

解：（Ⅰ）令x=1，y=0，
得f（1）·f（0）=f（1）+f（1），
又f（1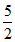）=，则f（0）=2，
令x=0，得f（0）·f（y）=f（y）+f（-y），
则f（y）=f（-y），又f（x）定义在R上，
故f（x）为偶函数；
（Ⅱ）a_n+1=2f（n+2）-f（n+1）
=2[f（n+1）·f（1）-f（n）]-f（n+1）
=4f（n+1）-2f（n），
而a_n=2f（n+1）-f（n），
故数列{a_n}是等比数列。

解析