题目

设函数f（x）=log_a（1-x），g（x）=log_a（1+x）（a＞0且a≠1），
（1）设F（x）=f（x）-g（x），判断F（x）的奇偶性并证明；
（2）若关于x的方程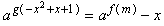有两个不等实根，求实数m的范围；
（3）若a＞1且在x∈[0，1]时，f（m-2x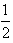）＞g（x）恒成立，求实数m的范围。

答案

解：（1），
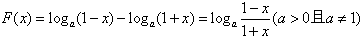其中，
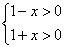∴x∈（-1，1），
，
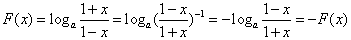∴F（x）为奇函数。
（2），
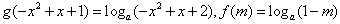原方程有两个不等实根即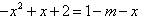有两个不等实根，
其中，
∴，
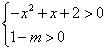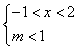即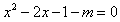在x∈（-1，2）上有两个不等实根。
记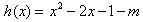，对称轴x=1，
由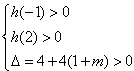，解得；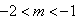
（3），
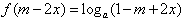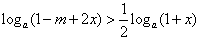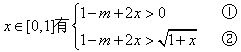即a＞1且x∈[0，1]时，恒成立，
∴恒成立，
由①得m＜1；
令，
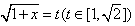∴由②得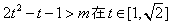时恒成立，
记，
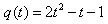即；
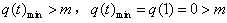综上m＜0。

解析