题目

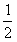设f（x）是定义在R上的偶函数，其图象关于直线x=1对称，对任意x₁，x₂∈[0，]都有f（x₁+x₂）=f（x₁）·f（x₂），
（Ⅰ）设f（1）=2，求；
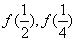（Ⅱ）证明f（x）是周期函数。

答案

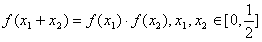（Ⅰ）解：由知，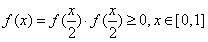
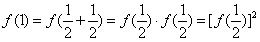∵，f（1）=2，
∴，
∵，，
∴。
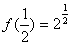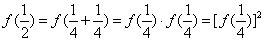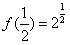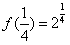（Ⅱ）证明：依题设y=f(x)关于直线x=1对称，故f(x)=f(1+1-x)，
即f(x)=f(2-x)，x∈R，
又由f(x)是偶函数知f(-x)=f(x)，x∈R，
∴f(-x)=f(2-x)，x∈R，
将上式中-x以x代换，得f(x)=f(x+2)，x∈R，
这表明f(x)是R上的周期函数，且2是它的一个周期。

解析