题目
(Ⅰ)讨论f(x)的奇偶性;
(Ⅱ)求f(x)的最小值。
答案
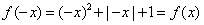 ,此时f(x)为偶函数;
,此时f(x)为偶函数;当a≠0时,
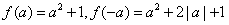 ,
,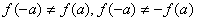 ,
,此时函数f(x)既不是奇函数,也不是偶函数。
(Ⅱ)(ⅰ)当x≤a时,函数
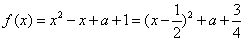 ,
,若
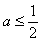 ,则函数f(x)在(-∞,a]上单调递减,
,则函数f(x)在(-∞,a]上单调递减,从而,函数f(x)在(-∞,a]上的最小值为
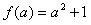 ;
;若
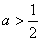 ,则函数f(x)在(-∞,a]上的最小值为
,则函数f(x)在(-∞,a]上的最小值为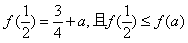 ;
; (ⅱ)当x≥a时,函数
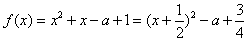 ;
;若
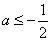 ,则函数f(x)在[a,+∞)上的最小值为
,则函数f(x)在[a,+∞)上的最小值为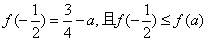 ;
;若
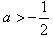 ,则函数f(x)在[a,+∞)上单调递增,
,则函数f(x)在[a,+∞)上单调递增,从而,函数f(x)在[a,+∞)上的最小值为
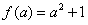 ;
;综上,当
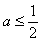 时,函数f(x)的最小值是
时,函数f(x)的最小值是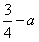 ;当
;当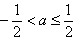 时,函数f(x)的最小值是
时,函数f(x)的最小值是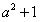 ;当
;当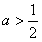 时,函数f(x)的最小值是
时,函数f(x)的最小值是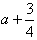 。
。