题目
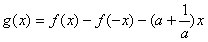 ,x∈R,a>0。
,x∈R,a>0。(1)判断函数g(x)的奇偶性,并说明理由;
(2)求函数g(x)的单调递增区间;
(3)证明:对任意实数x1和x2,且x1≠x2,都有不等式
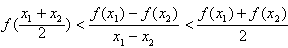 成立。
成立。 答案
且g(-x)=f(-x)-f(x)+
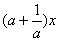

∴函数g(x)是奇函数。
(2)g"(x)=
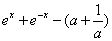
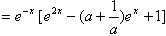
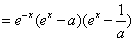
当a=1时,g"(x)=e-x(ex-1)2≥0当且仅当x=0时等号成立,
故 g(x)在R上递增;
当0<a<1时,
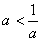 ,
,令g"(x)>0得
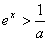 或ex<a,
或ex<a,故g(x)的单调递增区间为(-∞,lna)或(-lna,+∞);
当a>1时,
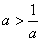 ,令g"(x)>0得ex>a或
,令g"(x)>0得ex>a或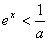
故g(x)的单调递增区间为(-∞,-lna)或(lna,+∞)。
(3)不妨设x1>x2,
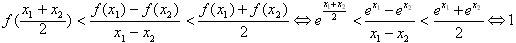
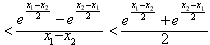
令
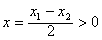 ,则只需证
,则只需证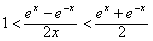
先证
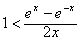 ,由(2)知
,由(2)知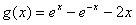 在R上递增,
在R上递增,∴当x>0时,g(x)>g(0)=0,
∴
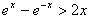 ,从而由x>0知
,从而由x>0知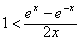 成立;
成立;再证
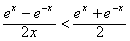 ,即证
,即证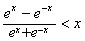
令
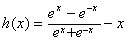 ,则
,则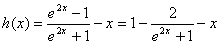 是减函数,
是减函数, ∴当x>0时,h(x)<h(0)=0,
从而
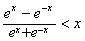 成立
成立综上,对任意实数x1和x2,且x1≠x2,都有不等式
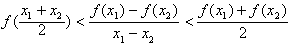 成立。
成立。