题目
(Ⅰ)求f(x)的表达式;
(Ⅱ)讨论g(x)的单调性,并求g(x)在区间[1,2]上的最大值与最小值。
答案
因此g(x)=f(x)+f′(x)=ax3+(3a+1)x2+(b+2)x+b,
因为函数g(x)是奇函数,所以g(-x)=-g(x),
即对任意实数x,有a(-x)3+(3a+1)(-x)2+(b+2)(-x)+b=-[ax3+(3a+1)x2+(b+2)x+b],
从而3a+1=0,b=0,
解得
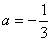 ,b=0,
,b=0,因此f(x)的解析表达式为
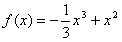 。
。(Ⅱ)由(Ⅰ)知
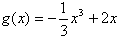 ,
,所以g′(x)=-x2+2,
令g′(x)=0,解得
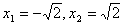 ,
,则当
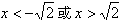 时,g′(x)<0,从而g(x)在区间
时,g′(x)<0,从而g(x)在区间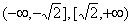 上是减函数;
上是减函数;当
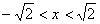 时,g′(x)>0,从而g(x)在区间
时,g′(x)>0,从而g(x)在区间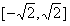 上是增函数;
上是增函数;由前面讨论知,g(x)在区间[1,2]上的最大值与最小值只能在x=1,
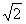 ,2时取得,
,2时取得,而
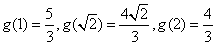 ,
,因此g(x)在区间[1,2]上的最大值为
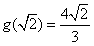 ,最小值为
,最小值为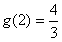 。
。 