题目

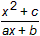已知函数f（x）=奇函数，f（1）＜f（3），且不等式0≤f（x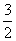）≤的解集是{x|-2≤x≤-1或2≤x≤4}。（1）求a，b，c的值；
（2）是否存在实数m使不等式f（-2+sinθ）＜-m²+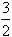对一切θ∈R成立？若存在，求出m的取值范围；若不存在，请说明理由。

答案

解；（1）∵f（x）是奇函数，
∴f（-x）=-f（x）对定义域内的一切x都成立，即b=0
从而f（x）=
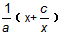
又∵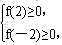即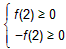
∴f（2）=0，解之，得c=-4
再由f（1）＜f（3），得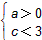或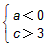，从而a＞0
此时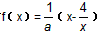在[2，4]上是增函数
注意到f（2）=0，则必有f（4）=
∴
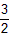
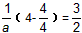
即a=2
综上可知，a=2，b=0，c=-4。
（2）由（1），得
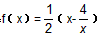
该函数在（-∞，0）以及（0，+∞）上均为增函数
又∵-3≤-2+sinθ≤-1，
∴f（-2+sinθ）的值域为
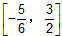
符合题设的实数m应满足＞
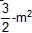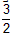
即m²＜0
故符合题设的实数m不存在。

解析