题目

已知函数f（x）的定义域为{x|x∈R，且x≠0}对定义域内的任意x₁，x₂，都有f （x₁·x₂）=f（x₁）+f（x₂），且当x>1时，f（x）>0，f（2）=1。
（1）求证：f（x）是偶函数；
（2）求证：f（x）在（0，+∞）上是增函数；
（3）解不等式：f（2x²-1）<2。

答案

解：（1）因对定义域内的任意x₁，x₂都有 f（x₁·x₂）=f（x₁）+f（x₂），
令x₁=x，x₂=-1，则有 f（-x）=f（x）+f（-1）
又令x₁=x₂=-1，得2f（-1）=f（1）
再令x₁=x₂=1，得f（1）=0，从而f（-1）=0，
于是有f（-x）=f（x）
∴f（x）是偶函数；
 （2）设0<x₁<x₂，则f（x₁）-f（x₂）=f（x₁）-
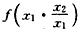
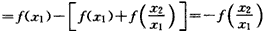
由于0<x₁<x₂
∴
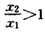
从而
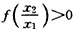
故f（x₁）-f（x₂）<0，即f（x₁）<f（x₂）
∴f（x）在（0，+∞）上是增函数；
（3）由于f（2）=1，
所以2=1+1=f（2）+f（2）=f（4），
于是待解不等式可化为f（2x²-1）<f（4）
结合（1），（2）已证结论，得上式等价于|2x²-1|<4
解得。

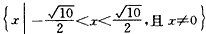解析