题目
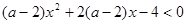 对一切
对一切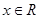 恒成立,试确定实数
恒成立,试确定实数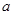 的取值范围.
的取值范围.
答案
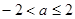 .
.
解析
试题分析:首先对二次项系数含参数的要讨论.当二次项系数不为零时,又由于是小于号连结的不等式的恒成立问题.等价于二次项系数小于零并且判别式小于零.本题别忘了对二次项系数分类.
试题解析:当
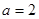 时,原不等式变形为
时,原不等式变形为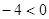 ,恒成立,即
,恒成立,即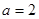 满足条件;
满足条件;当
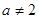 时,要使不等式
时,要使不等式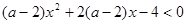 对一切
对一切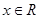 恒成立,
恒成立,必须
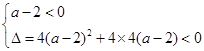 .解得,
.解得,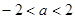 .综上所述,
.综上所述,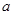 的取值范围是
的取值范围是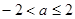 .
.
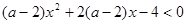 对一切
对一切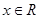 恒成立,试确定实数
恒成立,试确定实数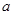 的取值范围.
的取值范围.
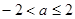 .
.
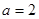 时,原不等式变形为
时,原不等式变形为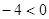 ,恒成立,即
,恒成立,即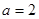 满足条件;
满足条件;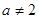 时,要使不等式
时,要使不等式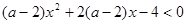 对一切
对一切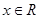 恒成立,
恒成立,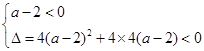 .解得,
.解得,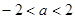 .综上所述,
.综上所述,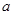 的取值范围是
的取值范围是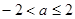 .
.