题目
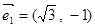 ,
,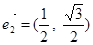 ,若
,若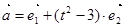 ,
,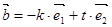 ,若
,若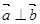 ,则实数
,则实数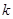 和
和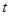 满足的一个关系式是 ,
满足的一个关系式是 ,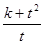 的最小值为 .
的最小值为 .
答案
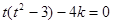 ,
,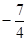 。
。
解析
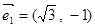 ,
,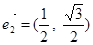 ,若
,若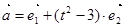 ,
,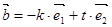 ,且有
,且有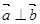 ,那么数量积为零,即
,那么数量积为零,即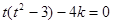 ,那么可知k,t的关系式,
,那么可知k,t的关系式,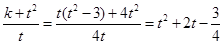 ,结合二次函数性质可知
,结合二次函数性质可知 最小值为
最小值为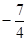 。
。解决该试题的关键是利用垂直关系得到k,t的关系式,然后消元法得到函数关系式进而求解最值。
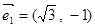 ,
,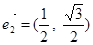 ,若
,若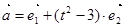 ,
,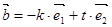 ,若
,若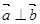 ,则实数
,则实数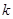 和
和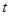 满足的一个关系式是 ,
满足的一个关系式是 ,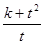 的最小值为 .
的最小值为 .
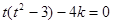 ,
,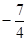 。
。
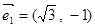 ,
,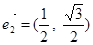 ,若
,若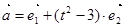 ,
,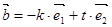 ,且有
,且有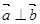 ,那么数量积为零,即
,那么数量积为零,即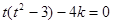 ,那么可知k,t的关系式,
,那么可知k,t的关系式,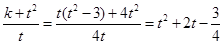 ,结合二次函数性质可知
,结合二次函数性质可知 最小值为
最小值为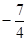 。
。