题目
已知二次函数
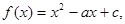 (其中
(其中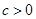 ).
).(1)若函数
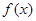 为偶函数,求
为偶函数,求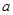 的值;
的值;(2)当
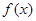 为偶函数时,若函数
为偶函数时,若函数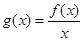 ,指出
,指出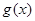 在
在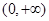 上单调性情况,并证明之.
上单调性情况,并证明之.
答案
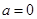 ;(2)见解析。
;(2)见解析。
解析
(1)
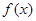 为偶函数,即对任意
为偶函数,即对任意 ,
,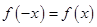
即
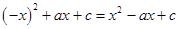 ,即
,即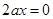 对任意
对任意 恒成立,得到a的值为零。
恒成立,得到a的值为零。(2)由(1),若
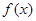 为偶函数,则
为偶函数,则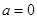 ,
,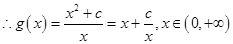
当
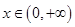 时,
时,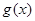 在
在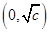 上单调递减,在
上单调递减,在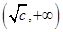 上单调递增,然后结合定义法证明。
上单调递增,然后结合定义法证明。解:(1)
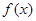 为偶函数,即对任意
为偶函数,即对任意 ,
,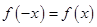 ……………2分
……………2分即
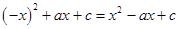 ,即
,即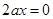 对任意
对任意 恒成立……………3分
恒成立……………3分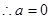 ……………4分
……………4分(2)由(1),若
 为偶函数,则
为偶函数,则 ,
,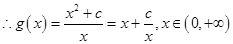
当
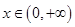 时,
时,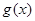 在
在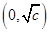 上单调递减,在
上单调递减,在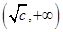 上单调递增,证明如下:……………5分
上单调递增,证明如下:……………5分设任意
 ,且
,且
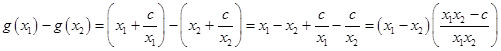 ……………7分
……………7分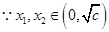 ,且
,且 ,
,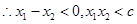 ,即
,即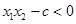
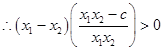 ,即
,即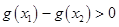 即
即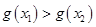
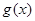 在
在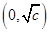 上单调递减 ……………9分
上单调递减 ……………9分同理,可得
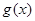 在
在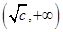 上单调递增 ……………10分
上单调递增 ……………10分
