题目
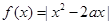
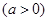 ,
,(1)当
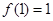 时, 求
时, 求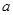 的值;
的值;(2)若函数
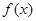 在
在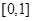 上的最大值为
上的最大值为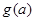
(ⅰ)求
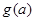 的解析式;
的解析式;(ⅱ)对任意的
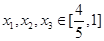 ,以
,以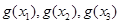 的值为边长的三条线段是否可构成三角形?请说明理由。
的值为边长的三条线段是否可构成三角形?请说明理由。
答案
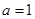 ;(2)
;(2)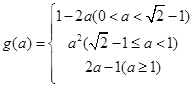 ;
;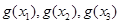 的值为边长的三条线段可构成三角形.
的值为边长的三条线段可构成三角形.
解析
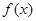 在
在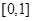 上单调性,数形结合;三条线段是否可构成三角形关键判断两边之和是否大于第三边。
上单调性,数形结合;三条线段是否可构成三角形关键判断两边之和是否大于第三边。解:1)、
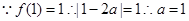 或
或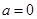 (舍去)
(舍去)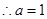
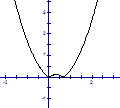
(2)(ⅰ)当
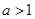 时,如图(1),
时,如图(1),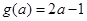
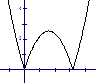
当
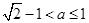 时,如图(2),
时,如图(2),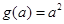
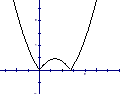
当
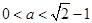 时,如图(2),
时,如图(2),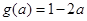
 |
|||||||||||
 |
 |
||||||||||
| |||||||||||
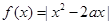
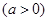 ,
,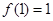 时, 求
时, 求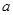 的值;
的值;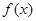 在
在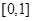 上的最大值为
上的最大值为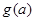
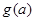 的解析式;
的解析式;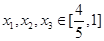 ,以
,以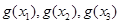 的值为边长的三条线段是否可构成三角形?请说明理由。
的值为边长的三条线段是否可构成三角形?请说明理由。
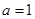 ;(2)
;(2)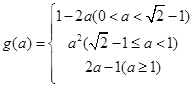 ;
;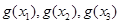 的值为边长的三条线段可构成三角形.
的值为边长的三条线段可构成三角形.
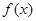 在
在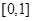 上单调性,数形结合;三条线段是否可构成三角形关键判断两边之和是否大于第三边。
上单调性,数形结合;三条线段是否可构成三角形关键判断两边之和是否大于第三边。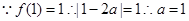 或
或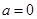 (舍去)
(舍去)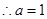
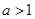 时,如图(1),
时,如图(1),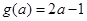
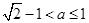 时,如图(2),
时,如图(2),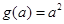
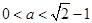 时,如图(2),
时,如图(2),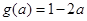
 |
|||||||||||
 |
 |
||||||||||
| |||||||||||