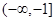题目
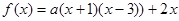 (
(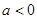 )
)(1)若方程
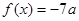 有两个相等的实数根,求
有两个相等的实数根,求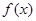 的解析式;
的解析式;(2)若函数
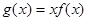 在区间
在区间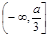 内单调递减,求a的取值范围
内单调递减,求a的取值范围
答案
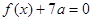 有两个相等的实数根,而
有两个相等的实数根,而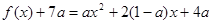 ,
,所以判别式△=
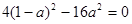 ,即
,即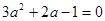
解得
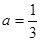 (舍去),或
(舍去),或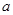 =-1,代入①式得
=-1,代入①式得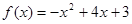 ……5分
……5分(Ⅱ)
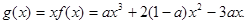
因为
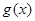 在区间
在区间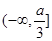 内单调递减,
内单调递减,所以
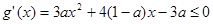 当
当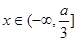 时恒成立……7分
时恒成立……7分∵
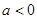 ,对称轴为直线
,对称轴为直线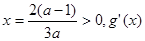 在
在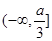 上为增函数,
上为增函数,故只需
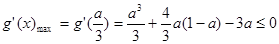 ……8分
……8分注意到
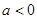 ,解得
,解得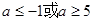 (舍去)。故
(舍去)。故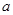 的取值范围是
的取值范围是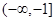
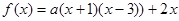 (
(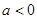 )
)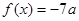 有两个相等的实数根,求
有两个相等的实数根,求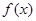 的解析式;
的解析式;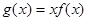 在区间
在区间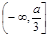 内单调递减,求a的取值范围
内单调递减,求a的取值范围
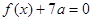 有两个相等的实数根,而
有两个相等的实数根,而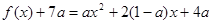 ,
,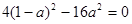 ,即
,即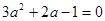
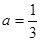 (舍去),或
(舍去),或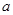 =-1,代入①式得
=-1,代入①式得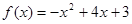 ……5分
……5分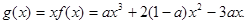
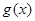 在区间
在区间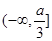 内单调递减,
内单调递减,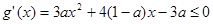 当
当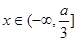 时恒成立……7分
时恒成立……7分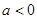 ,对称轴为直线
,对称轴为直线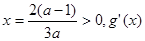 在
在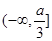 上为增函数,
上为增函数,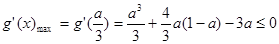 ……8分
……8分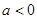 ,解得
,解得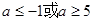 (舍去)。故
(舍去)。故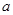 的取值范围是
的取值范围是