题目
已知
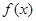 是定义在R上的不恒为零的函数,且对于任意的a,b∈R都满足:
是定义在R上的不恒为零的函数,且对于任意的a,b∈R都满足: 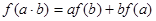 。
。(1)求f(0),f(1)的值;
(2)判断
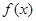 的奇偶性,并证明你的结论;
的奇偶性,并证明你的结论;(3)若
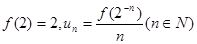 ,求数列{un}的前n项的和Sn 。
,求数列{un}的前n项的和Sn 。
答案
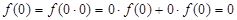 . 因为
. 因为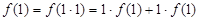 ,
,所以
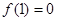 .
.(2)
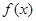 是奇函数. 证明:因为
是奇函数. 证明:因为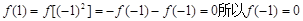 ,
, 因此,
因此,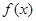 为奇函数.
为奇函数.(3)由
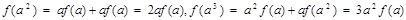 ,由此加以猜测
,由此加以猜测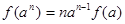 . 下面用数学归纳法证明:
. 下面用数学归纳法证明:1° 当n=1时,
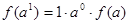 ,公式成立;
,公式成立;2°假设当n=k时,
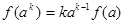 成立,那么当n=k+1时,
成立,那么当n=k+1时,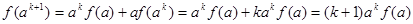 ,公式仍成立.
,公式仍成立.由上两步可知,对任意
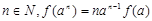 成立.所以
成立.所以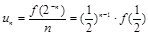 .
.因为
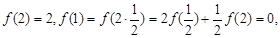 所以
所以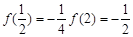 ,
,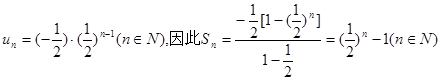 .
.
