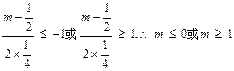题目
已知二次函数
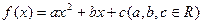 ,且同时满足下列条件:
,且同时满足下列条件:①
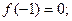 ② 对任意的实数
② 对任意的实数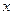 ,都有
,都有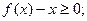
③ 当
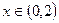 时,有
时,有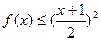 。
。(1)求
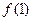 ;
; (2)求
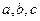 的值;
的值;(3)当
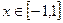 时,函数
时,函数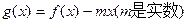 是单
是单 调函数,求
调函数,求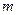 的取值范围。
的取值范围。
答案
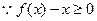 对一切
对一切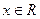 恒成立
恒成立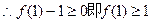
又
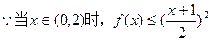
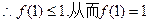
(2)
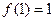 ,
,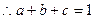 。又
。又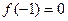

由
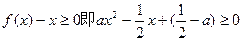 在R上恒成立,得
在R上恒成立,得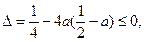
即
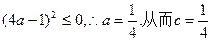 ,即
,即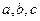 的值分别为
的值分别为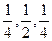 。
。(
 3)
3)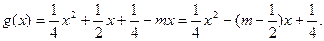
要使
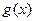 在
在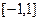
 上是单调函数,只要
上是单调函数,只要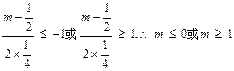
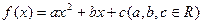 ,且同时满足下列条件:
,且同时满足下列条件: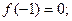 ② 对任意的实数
② 对任意的实数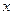 ,都有
,都有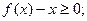
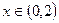 时,有
时,有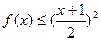 。
。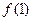 ;
; 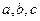 的值;
的值;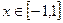 时,函数
时,函数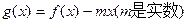 是单
是单 调函数,求
调函数,求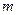 的取值范围。
的取值范围。
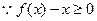 对一切
对一切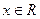 恒成立
恒成立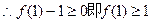
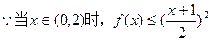
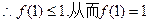
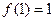 ,
,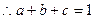 。又
。又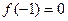

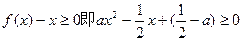 在R上恒成立,得
在R上恒成立,得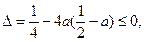
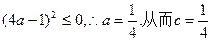 ,即
,即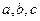 的值分别为
的值分别为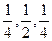 。
。 3)
3)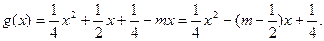
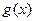 在
在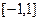
 上是单调函数,只要
上是单调函数,只要