题目
已知二次函数
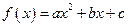 和“伪二次函数”
和“伪二次函数”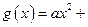
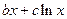 (
(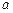 、
、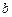 、
、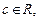
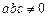 ),
),(I)证明:只要
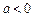 ,无论
,无论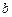 取何值,函数
取何值,函数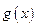 在定义域内不可能总为增函数;
在定义域内不可能总为增函数;(II)在二次函数
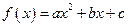 图象上任意取不同两点
图象上任意取不同两点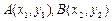 ,线段
,线段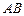 中点的横坐标为
中点的横坐标为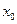 ,记直线
,记直线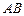 的斜率为
的斜率为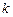 ,
, (
 i)求证:
i)求证: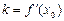 ;
;(ii)对于“伪二次函数”
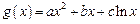 ,是否有(i)同样的性质?证明你的结论.
,是否有(i)同样的性质?证明你的结论.
答案
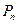 解:(I)如果
解:(I)如果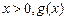 为增函数,
为增函数,则
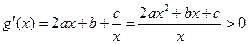 (1)恒成立,
(1)恒成立, 当
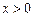 时恒成立,
时恒成立, 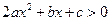 (2)
(2)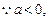 由二次函数的性质, (2)不可能恒成立.
由二次函数的性质, (2)不可能恒成立.则函数
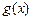 不可能总为增函数.--------3分
不可能总为增函数.--------3分(II)(i)
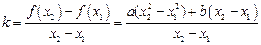 =
=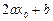 .
.由
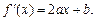
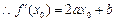 , 则
, 则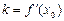 --------5分
--------5分(ii)不妨设
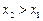 ,对于“伪二次函数”:
,对于“伪二次函数”: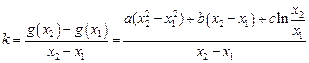
=
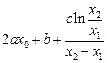 , (3) --------7分
, (3) --------7分由(ⅰ)中(1)
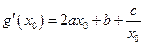 ,如果有(ⅰ)的性质,则
,如果有(ⅰ)的性质,则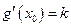 , (4)
, (4)比较(3)( 4)两式得
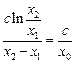 ,
,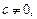
即:
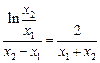 ,(4) --------10分
,(4) --------10分不妨令
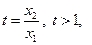
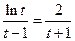 , (5)
, (5)设
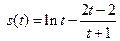 ,则
,则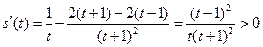 ,
,  ∴
∴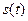 在
在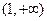 上递增, ∴
上递增, ∴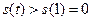 .
.∴ (5)式不可能成立,(4)式不可能成立,
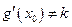 .
.∴“伪二次函数”
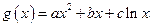 不具有(ⅰ)的性质. -------12分
不具有(ⅰ)的性质. -------12分
