题目
已知函数
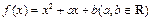 ,
,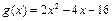 ,且
,且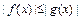 对
对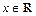 恒成立.
恒成立.(1)求a、b的值;
(2)若对
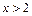 ,不等式
,不等式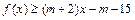 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.(3)记
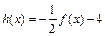 ,那么当
,那么当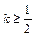 时,是否存在区间
时,是否存在区间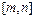 (
(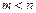 ),使得函数
),使得函数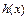 在区间
在区间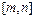 上的值域恰好为
上的值域恰好为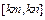 ?若存在,请求出区间
?若存在,请求出区间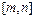 ;若不存在,请说明理由.
;若不存在,请说明理由.
答案
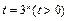 ,则
,则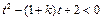 对
对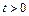 有解.
有解.记
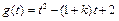 ,则
,则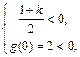 或
或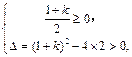 解得
解得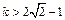 .
.21.解析:(1)由
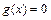 得
得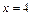 或
或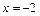 .于是,当
.于是,当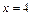 或
或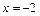 时,得
时,得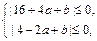
∴
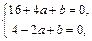 ∴
∴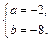 此时,
此时,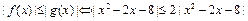 ,对
,对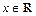 恒成立,满足条件.故
恒成立,满足条件.故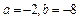 .
.(2)∵
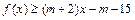 对
对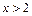 恒成立,∴
恒成立,∴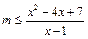 对
对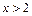 恒成立.
恒成立.记
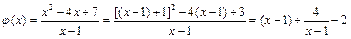 .∵
.∵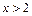 ,∴
,∴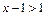 ,∴由对勾函数
,∴由对勾函数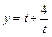 在
在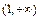 上的图象知当
上的图象知当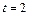 ,即
,即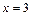 时,
时,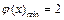 ,∴
,∴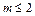 .
.(3)∵
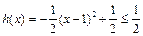 ,∴
,∴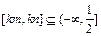 ,∴
,∴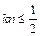 ,又∵
,又∵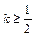 ,∴
,∴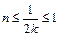 ,∴
,∴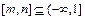 ,∴
,∴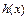 在
在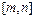 上是单调增函数,∴
上是单调增函数,∴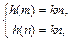 即
即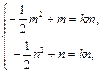 即
即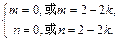 ∵
∵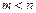 ,且
,且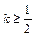 ,故:当
,故:当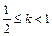 时,
时,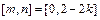 ;当
;当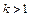 时,
时,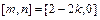 ;当
;当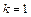 时,
时,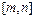 不存在.
不存在.
