题目
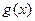 对任意实数
对任意实数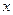 都满足
都满足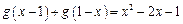 ,且
,且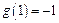 .令
.令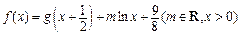 .
.(1)求
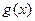 的表达式;
的表达式;(2)设
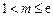 ,
,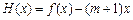 ,证明:对任意
,证明:对任意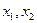
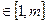 ,恒有
,恒有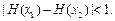
答案
(1)
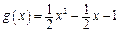
(2)略
解析
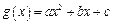 ,于是
,于是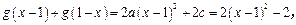
所以
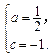 又
又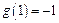 ,则
,则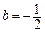 .所以
.所以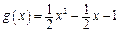 . ……………5分
. ……………5分(2)因为对
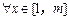 ,
,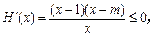 所以
所以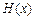 在
在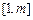 内单调递减.
内单调递减.于是
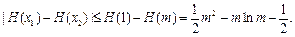 ……………8分
……………8分(到此可求高阶导数解之但下面方法更简)
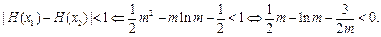
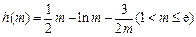 ,则
,则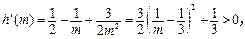
所以函数
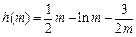 在
在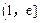 是单调增函数,
是单调增函数,所以
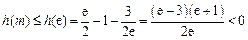 ,故命题成立.………… 13分
,故命题成立.………… 13分
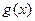 对任意实数
对任意实数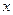 都满足
都满足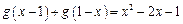 ,且
,且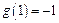 .令
.令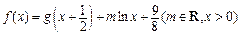 .
.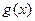 的表达式;
的表达式;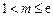 ,
,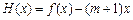 ,证明:对任意
,证明:对任意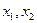
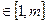 ,恒有
,恒有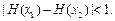
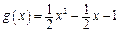
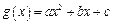 ,于是
,于是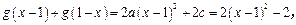
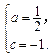 又
又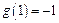 ,则
,则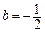 .所以
.所以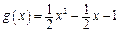 . ……………5分
. ……………5分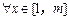 ,
,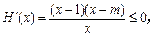 所以
所以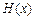 在
在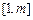 内单调递减.
内单调递减.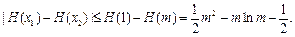 ……………8分
……………8分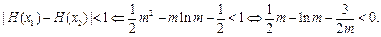
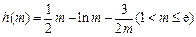 ,则
,则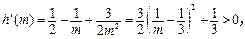
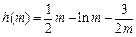 在
在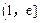 是单调增函数,
是单调增函数,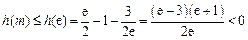 ,故命题成立.………… 13分
,故命题成立.………… 13分