题目

已知函数。
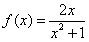(1)求函数的定义域；
(2)判断奇偶性；
(3)判断单调性；
(4)作出其图象，并依据图象写出其值域．

答案

解：（1）函数的定义域为R；
（2）∵，
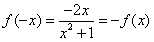∴f(x)是奇函数，其图象关于原点O对称。
（3）单调性：设x₁、x₂∈(0，+∞)且x₁＜x₂，
则，
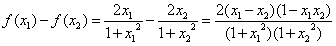当0＜x₁＜x₂≤1时，可知f(x₁)-f(x₂)＜0，
∴f(x)在(0，1]上是增函数，
当1＜x₁＜x₂时，f(x₁)-f(x₂)＞0，
∴f(x)在(1，+∞)上是减函数，
由于f(x)是奇函数，且f(0)=0，
因此，f(x)的减区间为(-∞，-1]、[1，+∞)，增区间为[-1，1]，并且当x→+∞时，f(x)→0，图象与x轴无限接近．
（4）其图象如下图所示，
，
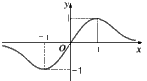可见其值域为[-1，1]．

解析