题目
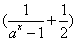 。
。(1)判断ψ(x)的奇偶性,并给出证明;
(2)证明:若xf(x)>0,则ψ(x)>0。
答案
(1)解:∵f(x)为奇函数,
∴f(-x)=-f(x),
又ψ(x)的定义域为{x∈R|x≠0},
则
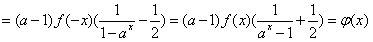 ,
,
∴ψ(x)是偶函数.
(2)证明:若x>0,则由已知,f(x)>0,这时
①当a>1时,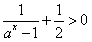 ,a-1>0,∴ψ(x)>0;
,a-1>0,∴ψ(x)>0;
②当0<a<1时,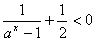 ,a-1<0,∴ψ(x)<0;
,a-1<0,∴ψ(x)<0;
又ψ(x)是偶函数,
∴x<0,ψ(x)=ψ(-x)>0,
故当xf(x)>0时,ψ(x)>0.
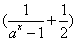 。
。(1)解:∵f(x)为奇函数,
∴f(-x)=-f(x),
又ψ(x)的定义域为{x∈R|x≠0},
则
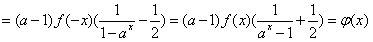 ,
,
∴ψ(x)是偶函数.
(2)证明:若x>0,则由已知,f(x)>0,这时
①当a>1时,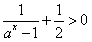 ,a-1>0,∴ψ(x)>0;
,a-1>0,∴ψ(x)>0;
②当0<a<1时,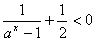 ,a-1<0,∴ψ(x)<0;
,a-1<0,∴ψ(x)<0;
又ψ(x)是偶函数,
∴x<0,ψ(x)=ψ(-x)>0,
故当xf(x)>0时,ψ(x)>0.