题目

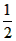已知f（x）在（-1，1）上有定义， f（）=1，且满足x，y∈（-1，1）时有
f（x）-f（y）=f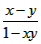（），数列{x_n}满足，
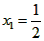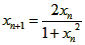
（I）求f（0）的值，并证明f（x）在（-1，1）上为奇函数；
（II）探索f（x_n+1）与f（x_n）的关系式，并求f（x_n）的表达式；
（III）是否存在自然数m，使得对于任意的n∈N*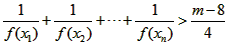，恒成立？若存在，求出m的最大值。

答案

解：（1）令x=y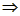f（0）=0；
已知f（x)在（-1，1）上有定义,
令x=0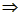f（0）-f（y）=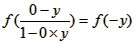
∴f(-y)=-f(y)
∴f（x）在（-1,1）上为奇函数；
（2）∵==
∴
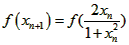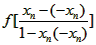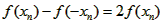
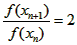
∴{f（x_n）}为等比数列
又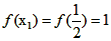，q=2
∴
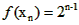
（3）假设存在自然数m满足题设条件，则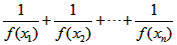
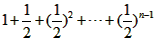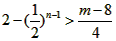==对于任意的n∈N*成立
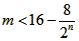∴对于任意的n∈N*成立，
当n=1时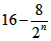，的最小值为12，
∴m<12，即m的最大值为11.

解析