题目
(1)求证:函数f(x)是偶函数;
(2)若f(x)在(-∞,0)上是增函数,判断f(x)在(0,+∞)的单调性。
答案
(1)证明:令x=y=0,则有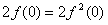 ,
,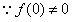 ,
,
∴f(0)=1,
令x=0,∴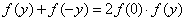 ,∴
,∴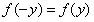 ,
,
∴f(x)是偶函数。
(2)解:令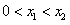 ,则
,则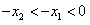 ,
,
∵f(x)在(-∞,0)上是增函数,
∴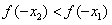 ,
,
又∵f(x)是偶函数,
∴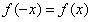 ,
,
∴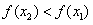 ,
,
∴f(x)在(0,+∞)上是减函数。
(1)证明:令x=y=0,则有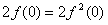 ,
,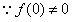 ,
,
∴f(0)=1,
令x=0,∴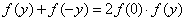 ,∴
,∴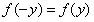 ,
,
∴f(x)是偶函数。
(2)解:令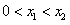 ,则
,则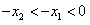 ,
,
∵f(x)在(-∞,0)上是增函数,
∴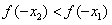 ,
,
又∵f(x)是偶函数,
∴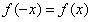 ,
,
∴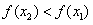 ,
,
∴f(x)在(0,+∞)上是减函数。