题目

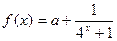(本小题满分13分)已知定义域为R的函数是奇函数．
（I）求a的值，并指出函数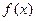的单调性（不必说明单调性理由）；
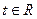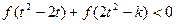（II）若对任意的，不等式恒成立，求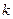的取值范围．

答案

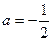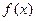（I），在R上为减函数
（II）

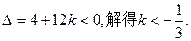
解析

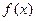解：（I）函数的定义域为R，因为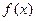是奇函数，所以，
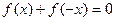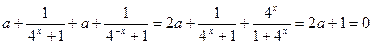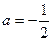即，故 ……4分
（另解：由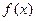是R上的奇函数，所以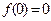，故．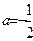
再由，
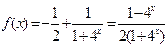通过验证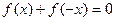来确定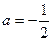的合理性）……………4分
由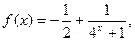知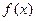在R上为减函数 ……………6分
（II）解法一：由（I）得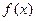在R上为减函数，
又因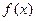是奇函数，从而不等式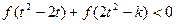等价于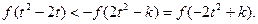
……………9分
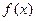在R上为减函数，由上式得：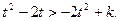
即对一切
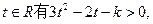
从而 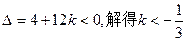……………13分
解法二：由（1）知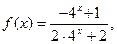又由题设条件得：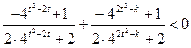
即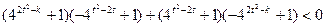……………9分
整理得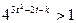，因底数4>1，故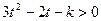
上式对一切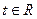均成立，从而判别式 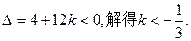…………13分